محاسبه رادیکال

اگر می‌خواهید اعداد رادیکالی از هر درجه را پیدا کنید، این ابزار محاسبه رادیکال دقیقاً برای شما طراحی شده است. این ابزار کاربردی فقط به دو مقدار نیاز دارد تا مقدار سوم را محاسبه کند.

اگر نمی‌دانید رادیکال چیست و می‌خواهید درباره نمادهای آن بیشتر بدانید، ادامه متن را بخوانید. در این متن تعریف رادیکال، مثال‌هایی از جمع و تفریق رادیکال‌ها، و پاسخ‌هایی به سوالات چگونه رادیکال‌ها را ضرب کنیم؟ و چگونه رادیکال‌ها را تقسیم کنیم؟ آورده شده است.

اگر به دنبال ساده‌ترین ریشه، یعنی ریشه دوم هستید، پیشنهاد می‌کنیم از ابزار محاسبه جذر ما استفاده کنید.

تعریف رادیکال

رادیکال به معنای جذر گرفتن از یک عدد است. این عمل معکوس توان محسوب می‌شود. در رادیکال، نماد رادیکال به صورت √ نمایش داده می‌شود و درجه رادیکال مشخص می‌کند که کدام ریشه از عدد گرفته شود. برای مثال:

عدد x تحت رادیکال با درجه n به صورت r نمایش داده می‌شود که برابر است با:

\(r = x^{1/n}\)

به عبارتی دیگر، رادیکال معکوس توان است که توان آن یک کسر می‌شود.

قوانین رادیکال

نمی‌توان ریشه هر عددی را محاسبه کرد. به طور کلی، عددی که می‌خواهید ریشه بگیرید باید مثبت باشد. اگر درجه رادیکال فرد باشد، می‌توان از اعداد منفی نیز ریشه گرفت. برای مثال:

\(\sqrt[3]{-8} = -2\)

درجه رادیکال (n) باید یک عدد صحیح مثبت باشد.

استفاده از ابزار محاسبه رادیکال

این ابزار شامل دو ورودی است که کار با آن بسیار ساده است. کافی است دو مقدار را وارد کرده و روی محاسبه یزنید، تا مقدار رادیکال محاسبه شود:

• عدد: عددی که می‌خواهید ریشه آن را پیدا کنید.
• درجه یا فرجه رادیکال: درجه رادیکال که معمولاً یک عدد صحیح مثبت است.

این ابزار به شما اجازه نمی‌دهد اعداد منفی وارد کنید، حتی اگر درجه رادیکال فرد باشد، زیرا ممکن است پاسخ‌های چندگانه یا اعداد مختلط ایجاد شود.

جمع و تفریق رادیکال‌ها

برای جمع و تفریق رادیکال‌ها، شرایط زیر باید برقرار باشد:

1. درجه رادیکال یکسان باشد.
2. عدد زیر علامت رادیکال یکسان باشد.

برای مثال:

• صحیح: \(2\sqrt{7} + 3\sqrt{7} = 5\sqrt{7}\)
• نادرست: \(\sqrt{7} + \sqrt{3} \neq \sqrt{10}\)

اگر این شرایط برقرار نباشد، می‌توانید عدد زیر علامت رادیکال را ساده کنید تا امکان جمع یا تفریق ایجاد شود.

مثال:

برای \(\sqrt{192}\) و \(\sqrt{3}\)، ابتدا \(\sqrt{192}\) را به صورت زیر ساده کنید:

\(\sqrt{192} = \sqrt{64 \times 3} = \sqrt{64} \times \sqrt{3} = 8\sqrt{3}\)

حالا:

\(8\sqrt{3} + \sqrt{3} = 9\sqrt{3}\)

ضرب رادیکال‌ها

برای ضرب رادیکال‌ها:

1. درجه رادیکال‌ها باید یکسان باشد.
2. اعداد زیر علامت رادیکال ضرب می‌شوند.

برای مثال:

\(\sqrt{7} \times \sqrt{4} = \sqrt{7 \times 4} = \sqrt{28}\)

اگر اعداد قبل از علامت رادیکال وجود داشته باشند، آن‌ها نیز ضرب می‌شوند:

\(2\sqrt{3} \times 4\sqrt{5} = (2 \times 4) \times \sqrt{3 \times 5} = 8\sqrt{15}\)

تقسیم رادیکال‌ها

برای تقسیم رادیکال‌ها:

1. درجه رادیکال‌ها باید یکسان باشد.
2. اعداد زیر علامت رادیکال تقسیم می‌شوند.

برای مثال:

\(\frac{\sqrt{8}}{\sqrt{4}} = \sqrt{\frac{8}{4}} = \sqrt{2}\)

اگر رادیکال‌ها درجات متفاوتی داشته باشند، می‌توانید آن‌ها را به صورت توان بازنویسی کرده و سپس عملیات را انجام دهید:

\(\frac{\sqrt[4]{2}}{\sqrt[3]{2}} = 2^{1/4} \div 2^{1/3} = 2^{1/4 – 1/3} = 2^{-1/12} = \frac{1}{\sqrt[12]{2}}\)

تابع و نمودار رادیکال 📈

ساده‌ترین تابع رادیکال به شکل زیر است:

\(f(x) = \sqrt[n]{x}\)

در اینجا:

• n درجه رادیکال است که معمولاً یک عدد صحیح مثبت است.

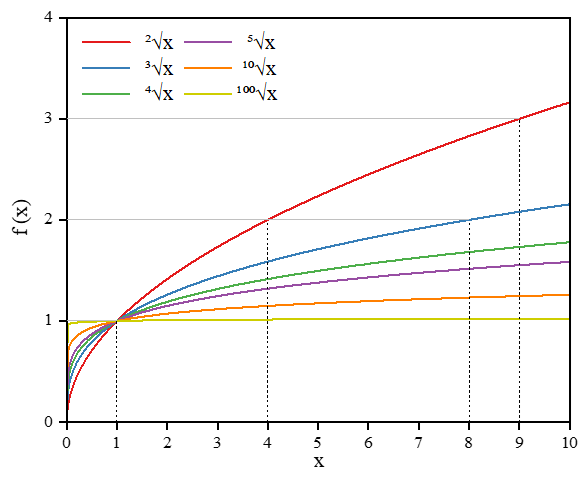
به طور خاص، اگر n=2 باشد، به یک جذر ساده (\(\sqrt{x}\)) می‌رسیم. در این حالت خاص، نیازی نیست عدد 2 را بالای نماد رادیکال بنویسید. نمودار این تابع رادیکال شبیه نیمه یک سهمی است که 90 درجه چرخیده باشد. همان‌طور که در تصویر زیر می‌بینید، با افزایش مقدار n، شکل نمودار رادیکال به تدریج صاف‌تر می‌شود.

نمودار تابع رادیکال برای درجات مختلف

می‌توان تابع رادیکال را بیشتر تعمیم داد و سه پارامتر اضافی به آن اضافه کرد:

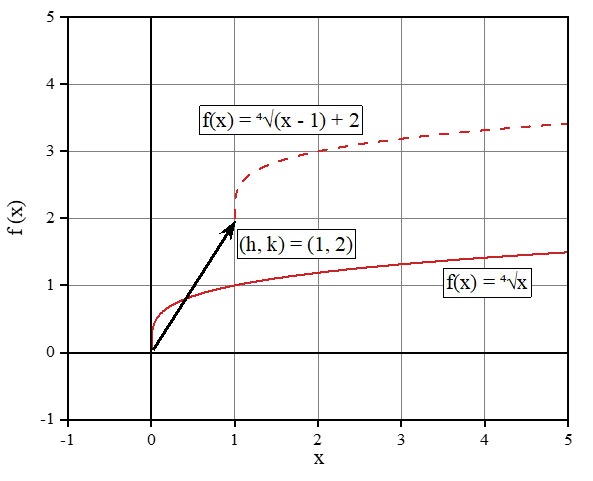
\(f(x) = a \cdot \sqrt[n]{b \cdot (x – h)} + k\)

در این رابطه:

• a: نمودار رادیکال را در محور y مقیاس‌بندی می‌کند.
• b: نمودار رادیکال را در محور x مقیاس‌بندی می‌کند.
• h: تابع رادیکال را در محور x جابه‌جا می‌کند.
• k: تابع رادیکال را در محور y جابه‌جا می‌کند.

درک تغییرات تابع رادیکال

شاید در ابتدا این رابطه پیچیده به نظر برسد 🤓، اما اگر به نمودار نگاه کنید، می‌توانید ببینید که پارامترهای h و k چگونه تابع رادیکال را جابه‌جا می‌کنند. به زبان ساده، این تابع توسط بردار (h, k) در صفحه مختصات انتقال پیدا می‌کند.

نکات اضافی در مورد رادیکال‌ها

• نمودارهای رادیکال فقط برای مقادیر مثبت x تعریف می‌شوند، مگر اینکه درجه رادیکال (n) فرد باشد. در این حالت، می‌توانید مقادیر منفی x را نیز در نظر بگیرید.
• برای درجات بالاتر (مانند n=3 یا n=4)، نمودار به تدریج صاف‌تر و گسترده‌تر می‌شود.
• پارامتر a می‌تواند باعث شود نمودار به سمت بالا یا پایین باز شود. اگر a منفی باشد، نمودار نسبت به محور x بازتاب می‌یابد.
• مقادیر b بزرگ‌تر باعث فشرده شدن نمودار در راستای محور x می‌شوند، در حالی که مقادیر b کوچک‌تر (بین 0 و 1) نمودار را کشیده می‌کنند.