محاسبه تجزیه به عوامل اول

ابزار تجزیه به عوامل اول، هر عددی را دریافت کرده و عوامل اول آن را پیدا می‌کند. کافی است عدد مورد نظر را وارد ابزار کرده و در کمترین زمان تجزیه به عوامل اول آن را محاسبه کنید. برای درک کامل این فرایند، ابتدا باید با مفهوم ضریب اول آشنا شوید. وقتی این را درک کردید، به تفاوت بین عامل اول و تجزیه اول خواهیم پرداخت.

در زیر، تمام پاسخ‌ها و اطلاعات مختصر در مورد نحوه پیدا کردن تجزیه اول و اینکه درخت عامل چیست را خواهید یافت.

عدد اول چیست؟

برای درک تجزیه به عوامل اول، باید از ابتدا شروع کنیم. عدد اول چیست؟ عددهای اول اعدادی هستند که تنها مقسوم‌علیه‌شان 1 و خود آن عدد است. به عبارت دیگر، نمی‌توان آن را با ضرب دو عدد طبیعی کوچکتر ساخت. نکته مهم این است که دو مقسوم‌علیه باید متفاوت باشند، بنابراین 1 عدد اول نیست زیرا هر دو مقسوم‌علیه 1 یکسان است. به عنوان مثال، 5 یک عدد اول است زیرا تنها مقسوم‌علیه‌های 5، 1 و 5 هستند. اما 6 عدد اول نیست، زیرا علاوه بر 1 و 6، مقسوم‌علیه‌های دیگری هم وجود دارند: 2 و 3.

اعداد اول به تعداد بی‌نهایت وجود دارند و هیچ فرمول ساده‌ای برای تعیین اینکه یک عدد اول است یا نه وجود ندارد. در صورت تمایل می‌توانید به ابزار محاسبه عدد اول هم سر بزنید!

ضریب (عامل) اول چیست؟

عوامل اول، مقسوم‌علیه‌های یک عددند که خودشان عدد اول هستند. به عنوان مثال، فرض کنید می‌خواهیم مقسوم‌علیه‌های 20 را پیدا کنیم، یعنی می‌خواهیم بدانیم چه اعداد صحیحی با هم ضرب شده و 20 را می‌دهند. می‌دانیم که 1 * 20 = 20، 2 * 10 = 20 و 4 * 5 = 20. اما توجه کنید که 20، 10 و 4 مقسوم‌علیه‌های اول نیستند. تنها مقسوم‌علیه‌های اول عدد 20، 2 و 5 هستند.

تجزیه به عوامل اول چیست؟

تجزیه به عوامل اول زمانی است که ما یک عدد را به عواملی که تنها عددهای اول هستند، تقسیم می‌کنیم. اگر به مثال بالا با عدد 20 نگاه کنیم، مقسوم‌علیه‌ها عبارتند از 1، 2، 4، 5، 10، 20. بهترین نقطه شروع، پیدا کردن حداقل یک عامل اولیه است که عدد اول باشد. از آنجا که 5 عدد اول است، می‌توانیم با 4 * 5 شروع کنیم. توجه کنید که 4 عدد اول نیست، بنابراین آن را به 2 * 2 تجزیه می‌کنیم. از آنجا که 2 عدد اول است، تجزیه اول 20 به صورت 2 * 2 * 5 خواهد بود. حالا می‌توانید این نتیجه را با ابزار محاسبه تجزیه به عوامل اول ما مقایسه کنید.

چگونه تجزیه به عوامل اول را پیدا کنیم؟

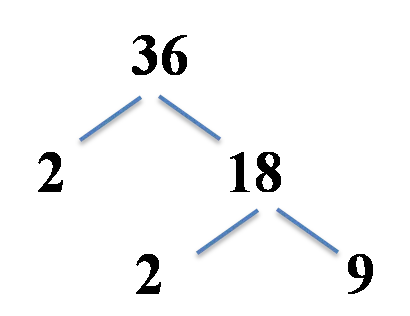
یک روش محاسبه تجزیه به عوامل اول، استفاده از نمودار درخت ضریب است، روشی آسان برای تقسیم یک عدد به عوامل اول آن. آماده‌اید؟

1. یک عدد انتخاب کنید. انتخاب عدد اول بی‌فایده است، زیرا تجزیه اول در همان نقطه تمام می‌شود. بیایید عدد 36 را انتخاب کنیم.
2. آن را به دو عدد تقسیم کنید، چه اول باشند و چه نه. ممکن است بخواهید تقسیمات ساده‌تری انجام دهید، مثلاً اگر عدد شما زوج است، آن را به 2 و عدد دیگر تقسیم کنید. 36 عدد زوج است، پس می‌توانیم آن را به صورت 2 * 18 بنویسیم.
3. شروع به ساخت درخت ضریب کنید. دو شاخه از عدد اصلی رسم کنید.

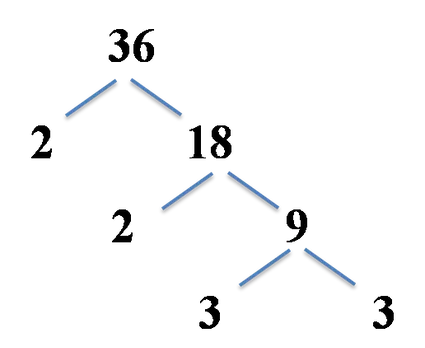
4. خط بعدی را تبدیل کنید. اگر عدد شما اول است، آن را همانطور که هست بگذارید. اگر عدد اول نیست، مرحله 2 را تکرار کنید.

5. مرحله 4 را تکرار کنید تا فقط اعداد اول باقی بمانند.

6. تجزیه اول نهایی و ضرایب اول را بنویسید.

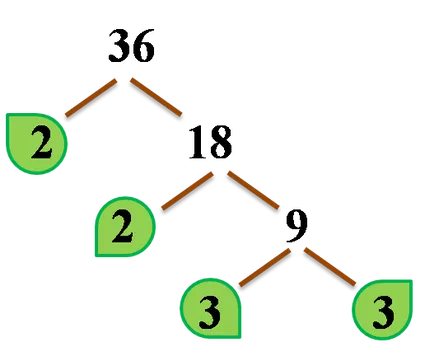
تمام برگ‌های درخت ضریب خود را بردارید و آن‌ها را با هم ضرب کنید:

36 = 2 * 2 * 3 * 3

این همان روشی است که ما برای پیدا کردن تجزیه به عوامل اول استفاده می‌کنیم!

عوامل اول عدد اصلی ما، 36، عبارتند از 2 و 3. ممکن است همان ضریب اول بیش از یک بار تکرار شود، همانطور که در مثال ما اتفاق افتاد. هر دو عدد اول دو بار در تجزیه اول ظاهر می‌شوند. سپس می‌توانیم آن را به صورت زیر بنویسیم:

36 = 2² * 3²

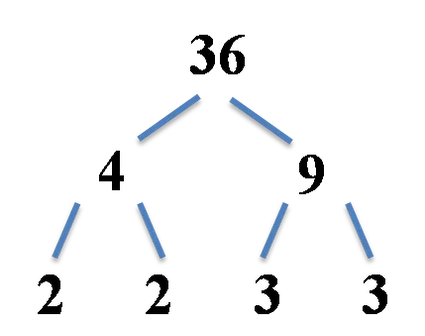
البته، شما باید با تقسیمات مختلف درخت عامل، نتیجه مشابهی بگیرید، مثلاً در اینجا:

بزرگترین مقسوم علیه مشترک

تجزیه به عوامل اول، اولین مرحله در یافتن تجزیه به عوامل اول است. بزرگترین ضریب دو یا چند عدد. تجزیه به عوامل اول به ویژه برای ساده‌سازی کسرها و حل معادلات با استفاده از چندجمله‌ای‌ها مفید است. به عنوان مثال، بزرگترین مقسوم علیه مشترک بین 6 و 20 عدد 2 است: تجزیه اول عدد اول 6 = 2 * 3 است، عدد دوم به صورت 20 = 5 * 2 * 2 نوشته می‌شود، و تنها عددی که در هر دو تجزیه اول ظاهر می‌شود 2 است. اگر می‌خواهید بزرگترین مقسوم علیه مشترک را به سرعت محاسبه کنید، از ابزار محاسبه ب.م.م ما استفاده کنید.

کوچک‌ترین مضرب مشترک

ابزار محاسبه تجزیه به عوامل اول همچنین برای یافتن کوچک‌ترین مضرب مشترک مفید است. کوچک‌ترین مضرب مشترک زمانی اهمیت دارد که بخواهید کسرهایی با مخرج‌های مختلف را جمع کنید. ک.م.م زمانی به دست می‌آید که توان‌های بالاتر از تمام عوامل میان دو عدد را ضرب کنید. به عنوان مثال، کمترین مضرب مشترک بین 6 و 20 برابر با (2 * 2 * 3 * 5) = 60 است. کمترین مضرب مشترک را می‌توان به صورت دستی یا با استفاده از ابزار محاسبه ک.م.م ما پیدا کرد.

محاسبه عوامل اول عدد…

در اینجا لیستی از عوامل اول برای راحتی شما آورده شده است. می‌توانید این مقادیر را با استفاده از ابزار تجزیه به عوامل اول ما تایید کنید.

• 2 عدد اول است
• 3 عدد اول است
• 4 = 2 × 2
• 5 عدد اول است
• 6 = 2 × 3
• 7 عدد اول است
• 8 = 2 × 2 × 2
• 9 = 3 × 3
• 10 = 2 × 5
• 11 عدد اول است
• 12 = 2 × 2 × 3
• 13 عدد اول است
• 14 = 2 × 7
• 15 = 3 × 5
• 16 = 2 × 2 × 2 × 2
• 17 عدد اول است
• 18 = 2 × 3 × 3
• 19 عدد اول است
• 20 = 2 × 2 × 5
• 21 = 3 × 7
• 22 = 2 × 11
• 23 عدد اول است
• 24 = 2 × 2 × 2 × 3
• 25 = 5 × 5
• 26 = 2 × 13
• 27 = 3 × 3 × 3
• 28 = 2 × 2 × 7
• 29 عدد اول است
• 30 = 2 × 3 × 5
• 31 عدد اول است
• 32 = 2 × 2 × 2 × 2 × 2
• 33 = 3 × 11
• 34 = 2 × 17
• 35 = 5 × 7
• 36 = 2 × 2 × 3 × 3
• 37 عدد اول است
• 38 = 2 × 19
• 39 = 3 × 13
• 40 = 2 × 2 × 2 × 5
• 41 عدد اول است
• 42 = 2 × 3 × 7
• 43 عدد اول است
• 44 = 2 × 2 × 11
• 45 = 3 × 3 × 5
• 46 = 2 × 23
• 47 عدد اول است
• 48 = 2 × 2 × 2 × 2 × 3
• 49 = 7 × 7
• 50 = 2 × 5 × 5
• 51 = 3 × 17
• 52 = 2 × 2 × 13
• 53 عدد اول است
• 54 = 2 × 3 × 3 × 3
• 55 = 5 × 11
• 56 = 2 × 2 × 2 × 7
• 57 = 3 × 19
• 58 = 2 × 29
• 59 عدد اول است
• 60 = 2 × 2 × 3 × 5
• 61 عدد اول است
• 62 = 2 × 31
• 63 = 3 × 3 × 7
• 64 = 2 × 2 × 2 × 2 × 2 × 2
• 65 = 5 × 13
• 66 = 2 × 3 × 11
• 67 عدد اول است
• 68 = 2 × 2 × 17
• 69 = 3 × 23
• 70 = 2 × 5 × 7
• 71 عدد اول است
• 72 = 2 × 2 × 2 × 3 × 3
• 73 عدد اول است
• 74 = 2 × 37
• 75 = 3 × 5 × 5
• 76 = 2 × 2 × 19
• 77 = 7 × 11
• 78 = 2 × 3 × 13
• 79 عدد اول است
• 80 = 2 × 2 × 2 × 2 × 5
• 81 = 3 × 3 × 3 × 3
• 82 = 2 × 41
• 83 عدد اول است
• 84 = 2 × 2 × 3 × 7
• 85 = 5 × 17
• 86 = 2 × 43
• 87 = 3 × 29
• 88 = 2 × 2 × 2 × 11
• 89 عدد اول است
• 90 = 2 × 3 × 3 × 5
• 91 = 7 × 13
• 92 = 2 × 2 × 23
• 93 = 3 × 31
• 94 = 2 × 47
• 95 = 5 × 19
• 96 = 2 × 2 × 2 × 2 × 2 × 3
• 97 عدد اول است
• 98 = 2 × 7 × 7
• 99 = 3 × 3 × 11
• 100 = 2 × 2 × 5 × 5
• 101 عدد اول است
• 102 = 2 × 3 × 17
• 103 عدد اول است
• 104 = 2 × 2 × 2 × 13
• 105 = 3 × 5 × 7
• 108 = 2 × 2 × 3 × 3 × 3
• 117 = 3 × 3 × 13
• 120 = 2 × 2 × 2 × 3 × 5
• 121 = 11 × 11
• 125 = 5 × 5 × 5
• 126 = 2 × 3 × 3 × 7
• 130 = 2 × 5 × 13
• 132 = 2 × 2 × 3 × 11
• 135 = 3 × 3 × 3 × 5
• 140 = 2 × 2 × 5 × 7
• 144 = 2 × 2 × 2 × 2 × 3 × 3
• 147 = 3 × 7 × 7
• 150 = 2 × 3 × 5 × 5
• 162 = 2 × 3 × 3 × 3 × 3
• 175 = 5 × 5 × 7
• 180 = 2 × 2 × 3 × 3 × 5
• 196 = 2 × 2 × 7 × 7
• 200 = 2 × 2 × 2 × 5 × 5
• 210 = 2 × 3 × 5 × 7
• 216 = 2 × 2 × 2 × 3 × 3 × 3
• 225 = 3 × 3 × 5 × 5
• 245 = 5 × 7 × 7
• 250 = 2 × 5 × 5 × 5
• 256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
• 300 = 2 × 2 × 3 × 5 × 5
• 375 = 3 × 5 × 5 × 5
• 400 = 2 × 2 × 2 × 2 × 5 × 5
• 500 = 2 × 2 × 5 × 5 × 5
• 625 = 5 × 5 × 5 × 5

در ابتدا، عدد 1 به عنوان یک عدد اول در نظر گرفته می‌شد. تا اوایل قرن 20، بیشتر ریاضیدان‌ها 1 را از مجموعه اعداد اول خارج کردند. توجه داشته باشید که ابزار ما، عدد 1 را در نتایج اعداد اول محاسبه نمی‌کند.