با ابزار محاسبه عدد اول ما میتوانید خیلی سریع و راحت بررسی کنید که آیا یک عدد خاص، اول است یا مرکب. در ادامه به سوالاتی مانند عدد اول چیست؟ و چگونه میتوان بررسی کرد که عددی اول است یا نه؟ پاسخ میدهیم. همچنین به نحوه یافتن اعداد اول و مفهوم اعداد نسبتاً اول یا متباین خواهیم پرداخت. همچنین توضیح میدهیم که آیا ۱، عدد اول است یا خیر و عجیبترین عدد اول کدام است.
عدد اول چیست؟
یک عدد طبیعی بزرگتر از 1 زمانی عدد اول نامیده میشود که دقیقاً دو مقسومعلیه داشته باشد، یعنی تنها بر 1 و خودش بخشپذیر باشد.
وقتی یک عدد طبیعی بزرگتر از 1 اول نباشد، عدد مرکب نامیده میشود.
اما خود عدد 1 چطور؟ عدد 1 نه اول است و نه مرکب، زیرا تنها یک مقسومعلیه دارد (خودش).
بیایید چند مثال بررسی کنیم:
- عدد
7اول است، زیرا تنها مقسومعلیههای آن1و7هستند. هیچکدام از اعداد قبل از7(2، 3، 4، 5 و 6) مقسومعلیه7نیستند، زیرا هیچکدام بدون باقیمانده بر7بخشپذیر نیستند. - عدد
8مرکب است، زیرا2یکی از مقسومعلیههای8است، و بنابراین8مقسومعلیههایی بیشتر از1و8دارد.
یک نکته جالب: عجیبترین عدد در بین اعداد اول، عدد 2 است، زیرا تنها عدد اول زوج است؛ بقیه اعداد اول همگی فرد هستند!
نحوه کار با ابزار محاسبه عدد اول ما
محاسبهگر اعداد اول ما بسیار ساده است. کافی است عددی را که میخواهید بررسی کنید وارد کرده و روی دکمه محاسبه بزنید. پاسخ به شما نمایش داده خواهد شد.
اگر عدد شما مرکب باشد، محاسبهگر کوچکترین مقسومعلیه غیر بدیهی (یعنی بزرگتر از 1) آن را به شما نشان میدهد.
چگونه بررسی کنیم که عددی اول است یا مرکب
سادهترین روش برای بررسی اینکه یک عدد صحیح n اول است، استفاده از الگوریتم آزمون تقسیم است: این روش شامل بررسی بخشپذیری n بر هر عدد بین 2 و n-1 است. این فرآیند محاسبات زیادی نیاز دارد. خوشبختانه، تعداد آزمونها را میتوان کاهش داد؛ کافی است بخشپذیری n را فقط بر اعداد اولی بررسی کنید که از √n تجاوز نمیکنند. نسخهای از همین الگوریتم در محاسبهگر اعداد اول ما استفاده میشود.
چگونه اعداد اول را پیدا کنیم
نمیتوانید تمام اعداد اول را پیدا کنید، زیرا اقلیدس حدود 300 سال قبل از میلاد اثبات کرد که تعداد اعداد اول بینهایت است.
اگر میخواهید تمام اعداد اول را تا یک حد مشخص، مثلاً n، پیدا کنید، میتوانید از الگوریتم معروف به غربال اراتوستن استفاده کنید:
- تمام اعداد از
2تاnرا بنویسید. - با کوچکترین عدد لیست، یعنی
2، شروع کنید. دور2را دایره بکشید و تمام مضارب متوالی آن (مثلاً4،6،8، …) را خط بزنید. - کوچکترین عددی که نه دایره کشیده شده و نه خط خورده است را پیدا کنید: این عدد
3است. دور3دایره کشیده و تمام مضارب بعدی آن (3،6،9، …) را خط بزنید. - همین روند را ادامه دهید: کوچکترین عدد موجود،
pرا پیدا کنید، دور آن دایره کشیده و تمام مضارب متوالی آن را خط بزنید. - اگر اعدادی بزرگتر از
pوجود دارند که هنوز خط نخوردهاند، به مرحله 4 برگردید. در غیر این صورت، کار تمام است.
اعدادی که دایره کشیده شدهاند، تمام اعداد اول کوچکتر از n هستند.
هر عددی که در هر مرحله از الگوریتم به p اختصاص داده شود، قطعاً اول است؛ زیرا در غیر این صورت، به عنوان مضرب یک عدد اول کوچکتر که قبلاً دایره کشیده شده است، خط خورده بود.
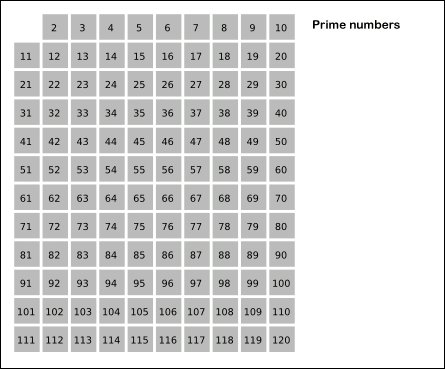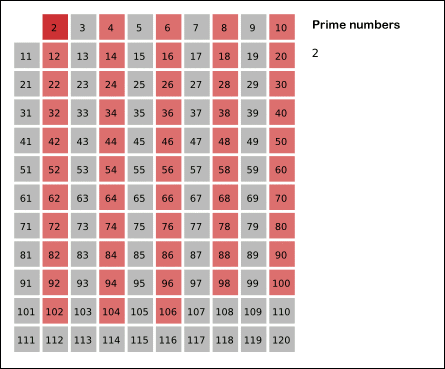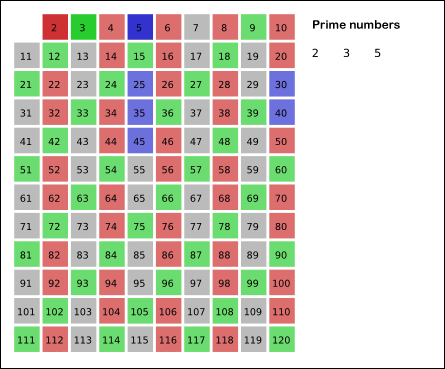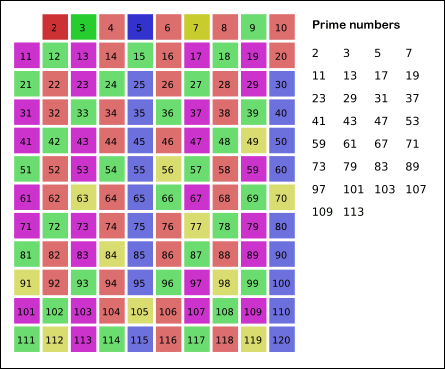
در انیمیشن زیر، میتوانید مشاهده کنید که غربال اراتوستن چگونه تمام اعداد اول تا 120 را پیدا میکند.
راهنمای رنگها:
- قرمز: مضربهای
2 - سبز: مضربهای
3 - آبی: مضربهای
5 - زرد: مضربهای
7 - و اعداد باقیمانده بنفشرنگ، اعداد اول هستند.
همانطور که میتوانید تصور کنید، برای اعداد واقعاً بزرگ، تعیین اینکه اول هستند یا مرکب، چالشبرانگیز است. بنابراین، روشهای بسیار پیچیدهای مورد نیاز است. جالب است بدانید جستجوی اعداد اول بزرگ همچنان ادامه دارد: تا مارس 2020، بزرگترین عدد اول شناخته شده دارای 24,862,048 رقم است!
چرا اعداد اول مهم هستند؟
اعداد اول در نظریه اعداد بسیار اهمیت دارند، زیرا طبق قضیه اساسی حساب، هر عدد طبیعی بزرگتر از 1 میتواند به شکلی یکتا (صرف نظر از ترتیب ضرب) به صورت حاصل ضرب اعداد اول نوشته شود. به عبارت دیگر، اعداد اول بلوکهای سازنده تمام اعداد طبیعی دیگر هستند. برای آشنایی با این مورد، ابزار تجزیه به عوامل اول را مشاهده کنید.
در واقع، این قضیه یکی از دلایل اصلی است که نمیخواهیم 1 به عنوان یک عدد اول شناخته شود.
اگر 1 اول بود، تجزیه عدد به عوامل اول دیگر یکتا نبود، زیرا مثلاً میداشتیم:
6 = 2 × 3 = 1 × 2 × 3 = 1 × 1 × 2 × 3 = ...
از کاربردهای عملی اعداد اول، میتوان به استفاده از آنها را در پروتکلهای رمزنگاری مانند رمزنگاری RSA اشاره کرد.
اعداد نسبت به هم اول
مفهوم اعداد اول را با اعداد متباین یا نسبت به هم اول اشتباه نگیرید! دو عدد طبیعی وقتی نسبت به هم اول (یا کوپریم) هستند که هیچ عدد صحیحی غیر از 1 وجود نداشته باشد که هر دو عدد را بخشپذیر کند. به عبارت دیگر، بزرگترین مقسومعلیه مشترک (GCF) آنها برابر 1 است.
18و30نسبت به هم اول نیستند، زیرا هر دو بر3بخشپذیر هستند و بزرگترین مقسوم علیه مشترک آنها برابر با6است.18و35نسبت به هم اول هستند: مقسومعلیههای18عبارتند از 1، 2، 3، 6، 9، 18 و مقسومعلیههای35عبارتند از 1، 5، 7، 35. تنها مقسومعلیه مشترک آنها1است.
یادتان باشد:
- دو عدد اول همیشه نسبت به هم اول هستند.
- نیازی نیست اعداد اول باشند تا نسبت به هم اول باشند!
برای کسب اطلاعات بیشتر، به ابزار محاسبه اعداد متباین یا نسبت به هم اول ما مراجعه کنید.