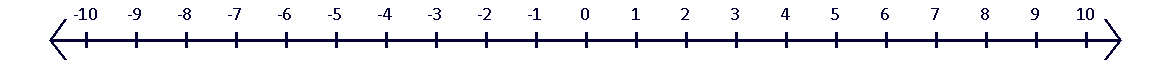محاسبه اعداد صحیح

به ابزار محاسبات اعداد صحیح سایت آریاکیت خوش آمدید، جایی که در آن با تمام عملیات‌های پایه ریاضی آشنا خواهیم شد: جمع و تفریق اعداد صحیح، ضرب و تقسیم اعداد صحیح. سپس به سراغ عملیات‌های پیچیده‌تر مانند توان، جذر و لگاریتم خواهیم رفت. به یاد داشته باشید که تعریف عدد صحیح فقط شامل اعداد صحیح مثبت نمی‌شود، بنابراین این ابزار به عنوان ماشین حساب اعداد منفی نیز عمل می‌کند.

عدد صحیح در ریاضی چیست؟ چه چیزی باعث می‌شود که مربع یک عدد منفی یا لگاریتم یک عدد منفی معنای مشخصی داشته باشد؟

در ادامه به این سوالات پاسخ می‌دهیم!

🙋 برای دیدن سایر ابزارهای ریاضی، به بخش ابزار ریاضی ما مراجعه کنید.

عدد صحیح در ریاضی چیست؟

به طور عامیانه، یک عدد صحیح یک عدد کامل است. به عبارت دیگر، شامل کسرها یا اعداد گنگ مانند π از محاسبات دایره نمی‌شوند. نمونه‌های زیر همگی اعداد صحیح هستند:

• 2, 2021, 13, -17, -173,029, 0, 1,000,000,000

توجه داشته باشید که:

• تمام اعداد صحیح مثبت، هر چقدر هم که طولانی باشند، اعداد صحیح هستند: ما گاهی آن‌ها را اعداد طبیعی هم می‌نامیم.
• صفر نیز یک عدد صحیح است.
• اعداد صحیح شامل اعداد منفی هستند به شرطی که کسر نباشند.

تعریف رسمی عدد صحیح به شرح زیر است:

💡 عدد صحیح، هر عدد حقیقی است که بدون بخش کسری می‌توانیم آن را بنویسیم.

بیایید کلمه «می‌توانیم» در تعریف عدد صحیح بالا را تاکید کنیم. توجه کنید که کسر ساده 4/2 برابر با 2 است، بنابراین آن نیز یک عدد صحیح است که از ساده‌سازی کسر حاصل می‌شود، اگرچه در نگاه اول چنین به نظر نمی‌رسد.

محور اعداد منفی و مثبت

اعداد صحیح (و تمام اعداد حقیقی دیگر) روی یک محور بی‌نهایت به نام محور اعداد ظاهر می‌شوند.

در واقع، این محور به ما می‌گوید که یک عدد نسبت به سایر اعداد کجا قرار دارد: بزرگ‌تر (به سمت راست) یا کوچک‌تر (به سمت چپ) از عدد دیگر است؟

اعداد منفی عکس اعداد مثبت هستند که محور تقارن آن‌ها در نقطه صفر قرار دارد. به عبارت دیگر، اگر از صفر شروع کنیم و به راست برویم، عدد 1 را می‌بینیم، سپس 2، 3 و به همین ترتیب. از طرف دیگر، اگر به سمت چپ برویم، همان اعداد را می‌بینیم اما با منفی‌ها: -1، سپس -2، -3 و به همین ترتیب. پس، یک عدد و منفی آن در فاصله‌ای برابر از صفر قرار دارند اما در طرف‌های مقابل (این فاصله به نام مقدار مطلق عدد شناخته می‌شود).

ویژگی‌های حسابی و جبر از جمله جمع، تفریق، ضرب، تقسیم، توان، ریشه، لگاریتم و غیره بر روی تمامی اعداد روی خط عددی منفی و مثبت قابل اعمال است.

جمع و تفریق اعداد صحیح

هنگام جمع و تفریق اعداد صحیح، خوب است که خط عددی منفی و مثبت را که در بخش بالا بیان شد در ذهن داشته باشیم.

فرض کنید که اعداد صحیح a و b را داریم، و ببینیم چگونه می‌توانیم a + b و a - b را پیدا کنیم.

برای پیدا کردن a + b، به اندازه b از a جابجا شوید:

• به سمت راست، اگر b مثبت باشد.
• به سمت چپ، اگر b منفی باشد.

برای پیدا کردن a - b، به اندازه b از a جابجا شوید:

• به سمت چپ، اگر b مثبت باشد.
• به سمت راست، اگر b منفی باشد.

چند مثال از جمع و تفریق اعداد صحیح در زیر آمده است:

• 3 + 4 = 7
• -5 + 9 = 4
• 10 + (-12) = 10 - 12 = -2
• -3 + (-7) = -3 - 7 = -10
• 4 - 5 = -1
• 3 - (-2) = 3 + 2 = 5
• -10 - (-4) = -10 + 4 = -6

مشاهده کنید که هرگاه دو علامت کنار هم داریم، باید عدد منفی را در پرانتز قرار دهیم. علاوه بر این، در این مواقع می‌توان دو علامت را به یک علامت تبدیل کرد طبق قوانین زیر:

• + و + نتیجه + می‌دهد
• + و - نتیجه - می‌دهد
• - و + نتیجه - می‌دهد
• - و - نتیجه + می‌دهد.

ضرب و تقسیم اعداد صحیح

در اصل، قوانین منفی و مثبت برای ضرب اعداد صحیح و تقسیم اعداد صحیح تقریباً یکسان هستند. تنها چیزی که باید در نظر بگیریم علامت‌ها هستند. به طور دقیق‌تر، علامت نتیجه، به علامت‌های عوامل ضرب یا مقسوم و مقسوم‌علیه در تقسیم بستگی دارد.

در زیر چند مثال از ضرب اعداد صحیح و سپس تقسیم آمده است:

• 6 × 8 = 48
• -4 × 5 = -20
• 10 × (-2) = -20
• (-1) × (-8) = 8
• 12 / 4 = 3
• 24 / (-8) = -3
• -7 / (-2) = 3.5

این پایان عملیات‌های پایه چهارگانه است که توسط ابزار محاسبه اعداد صحیح ما پوشش داده شده است. حالا به سمت عبارات جبر پیچیده‌تر (اما هنوز ساده!) می‌رویم.

توان، جذر، لگاریتم

توان

برای توان‌های اعداد صحیح مثبت، قوانین اعداد منفی و مثبت همانند هم هستند: نتیجه فقط عددی است که چندین بار ضرب می‌شود. و ما قبلاً دیدیم که چگونه ضرب اعداد صحیح در بخش قبلی کار می‌کند، بنابراین بیایید فقط چند مثال را ذکر کنیم:

• 43 = 4 × 4 × 4 = 64
• (-3)4 = (-3) × (-3) × (-3) × (-3) = 81
• (-2)5 = (-2) × (-2) × (-2) × (-2) × (-2) = -32

مشاهده کنید که برای پایه‌های با توان منفی، علامت نتیجه به زوج یا فرد بودن توان بستگی دارد. این یک نتیجه مستقیم از قوانین اعداد منفی و مثبت در بخش جمع و تفریق اعداد صحیح است. به طور خاص، مربع یک عدد منفی همیشه یک مقدار مثبت خواهد داد.

حال، اگر توان منفی باشد، ابتدا علامت منفی آن را با تغییر پایه به معکوس آن از بین می‌بریم: a-b = (1/a)b

به عنوان مثال:

• 4-3 = (¼)3 = ¼ × ¼ × ¼ = 1/64
• (-3)-4 = (-⅓)4 = (-⅓) × (-⅓) × (-⅓) × (-⅓) = 1/81
• (-2)-5 = (-½)5 = (-½) × (-½) × (-½) × (-½) × (-½) = -1/32

جذر

گرفتن ریشه (که به آن رادیکال یا جذر نیز گفته می‌شود) عملی مخالف توان است. بنابراین، برخی قوانین برای هر دو اعمال می‌شود. مهم‌ترین نکته این است که برای توان‌ها، توان‌های زوج همیشه نتیجه‌ای مثبت می‌دهند، صرف نظر از علامت پایه. اگر این ویژگی را برای ریشه‌ها ترجمه کنیم، متوجه خواهیم شد که رادیکال‌های با درجه زوج فقط برای اعداد مثبت وجود دارند. نمی‌توانیم ریشه مربع یک عدد منفی را داشته باشیم. در حقیقت، چنین اعدای وجود دارند، اما دیگر اعداد حقیقی نیستند بلکه اعداد مختلط هستند.

بیایید چند مثال از ریشه‌های اعداد صحیح را بررسی کنیم:

• ∜256 = 4
• ∛(-125) = -5

لگاریتم‌ها

لگاریتم‌ها فقط برای اعداد مثبت تعریف شده‌اند. به عبارت دیگر، چیزی به نام لگاریتم یک عدد منفی وجود ندارد. مشابه ریشه‌ها، در حقیقت چنین چیزی وجود دارد، اما فراتر از اعداد حقیقی است و داستان به شدت پیچیده می‌شود.

بیایید این بخش را با چند مثال از لگاریتم‌های اعداد صحیح مثبت به پایان برسانیم:

• log101000 = 3
• log96561 = 4
• log2128 = 7

استفاده از ابزار محاسبه اعداد صحیح

در بالای ابزار، عملیاتی را که می‌خواهید انجام دهید انتخاب کنید. هفت گزینه وجود دارد:

• جمع
• تفریق
• ضرب
• تقسیم
• توان
• جذر
• لگاریتم

پس از انتخاب عملیات، فرمول نمادین با متغیرهای a و b در زیر آن ظاهر می‌شود.

پس از مشاهده فرمول، مقادیر a و b را در فیلدهای مربوطه وارد کنید.

با زدن دکمه محاسبه، نتیجه نمایش داده خواهد شد.