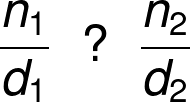این ابزار مقایسه کسرها به شما کمک میکند کسرهای ساده، کسرهای مرکب، اعداد مخلوط، یا حتی اعداد کامل را از نظر بزرگی و کوچکی با هم مقایسه کنید. نیازی نیست کسرهای شما مخرج مشترک داشته باشند، این ابزار حتی برای مقایسه کسرهایی با مخرجهای متفاوت بهخوبی عمل میکند.
چگونه کسرها را مقایسه کنیم؟
دو روش محبوب وجود دارد که میتوانید برای مقایسه کسرها استفاده کنید:
- روش اعشاری، که در آن هر کسر به عدد اعشاری تبدیل میشود. این کار با یک ماشین حساب جیبی ساده امکانپذیر است، بنابراین در اینجا وارد جزئیات نمیشویم.
- روش مخرج یکسان، که در ادامه بهطور کامل توضیح داده شده است، زیرا به احتمال زیاد دنبال این روش هستید 😉
در روش مخرج یکسان، چند حالت ممکن است رخ دهد:
- مقایسه کسرها با مخرج یکسان، که البته سادهترین حالت است 😀
- مقایسه کسرها با صورت یکسان، این هم مشکل پیچیدهای نیست 🙂
- مقایسه کسرها با مخرجهای متفاوت، ممکن است کمی دشوارتر به نظر برسد، چون نیاز به پیدا کردن مخرج مشترک دارید. اما هنوز هم ساده است، به ما اعتماد کنید! 🍰
مقایسه کسرها با مخرج یکسان
مقایسه کسرها با مخرج یکسان سادهترین گزینه است. اگر دو کسر شما مخرج یکسان داشته باشند (عدد پایین)، کسر بزرگتر کسری است که صورت (عدد بالا) بزرگتری دارد. برای مثال:
4/5 > 3/5
چون
4 > 3
و:
3/7 < 6/7
چون
3 < 6
یک مثال بزنیم:
ما تعداد زیادی برش پیتزا 🍕 داریم و هر برش به یک اندازه است. چه کسی برشهای بیشتری دارد، مایکل با 3 برش یا امیلی با 2 برش؟ اگر هر پیتزا به 8 قسمت مساوی تقسیم شده باشد:
3/8 > 2/8
قطعا مایکل! چرا که سه برش 🍕🍕🍕 بیشتر از دو برش 🍕🍕 است.
مقایسه کسرها با صورت یکسان
حال، اگر دو کسر صورت یکسان داشته باشند چه میشود؟ در این حالت، کسر بزرگتر کسری است که مخرج کوچکتری دارد. بهعنوان مثال:
4/5 > 4/7
و:
3/11 < 3/8
به مثال پیتزا برگردیم:
امیلی خوشش نیامد که مایکل برشهای بیشتری داشت. بنابراین گفت که دفعه بعد همه باید تعداد برشهای یکسانی داشته باشند، اما نقشه زیرکانه او این بود که اندازه برشها برابر نباشد 😈. او یک پیتزا را به 8 قسمت تقسیم کرد و 3 برش به مایکل داد، و پیتزای دیگری را به 4 قسمت تقسیم کرد و 3 برش برای خودش برداشت. چه کسی پیتزای بیشتری دارد؟ پاسخ این است:
3/8 < 3/4
امیلی سه برش بزرگتر برداشته، بنابراین قطعا بیشتر از مایکل پیتزا دارد!
مقایسه کسرها با مخرجهای متفاوت
چگونه کسرها را با مخرجهای متفاوت مقایسه کنیم؟ بهعنوان مثال 3/8 و 1/6. دو روش برای یکسان کردن مخرج وجود دارد:
- روش مخرج مشترک: که در آن صورت و مخرج هر کسر را در مخرج کسر دیگر ضرب میکنید:
3/8 ? 1/6
(3/8) × (6/6) ? (1/6) × (8/8)
18/48 > 8/48
روش دوم:
- روش کمترین مخرج مشترک (ک.م.م): که در آن کوچکترین مضرب مشترک مخرجها را پیدا کرده و کسرهای معادل را با آن مخرج محاسبه میکنید:
3/8 ? 1/6
LCM(8,6) = 24
9/24 > 4/24
هر دو روش مشابه هستند و میتوانید هر کدام را که ترجیح میدهید استفاده کنید.
🔎 قصد دارید کارهای بیشتری با کسرها انجام دهید؟ ابزار آنلاین زیر را از دست ندهید: